Nonlinear models

EC 320, Set 08

Andrew Dickinson

Spring 2023

Prologue

Housekeeping

PS04:

  • Due next Tuesday night

LA07:

  • Due Friday at 5:00p

Reading: (up to this point)

ItE: R, 1, 2, 3, 4

MM: 1, 2

Linear regression

Suppose we would like to estimate the degree to which an increase in GDP correlates with Life expectancy. We set up our model as follows:

\[ {\text{Life Expectancy}_i} = \beta_0 + \beta_1 \text{GDP}_i + u_i \]

Using the gapminder, we could quickly generate estimates to get at the correlation But first, as always, let’s plot it before running the regression

Visualize the OLS fit? Is \(\beta_1\) positive or negeative?

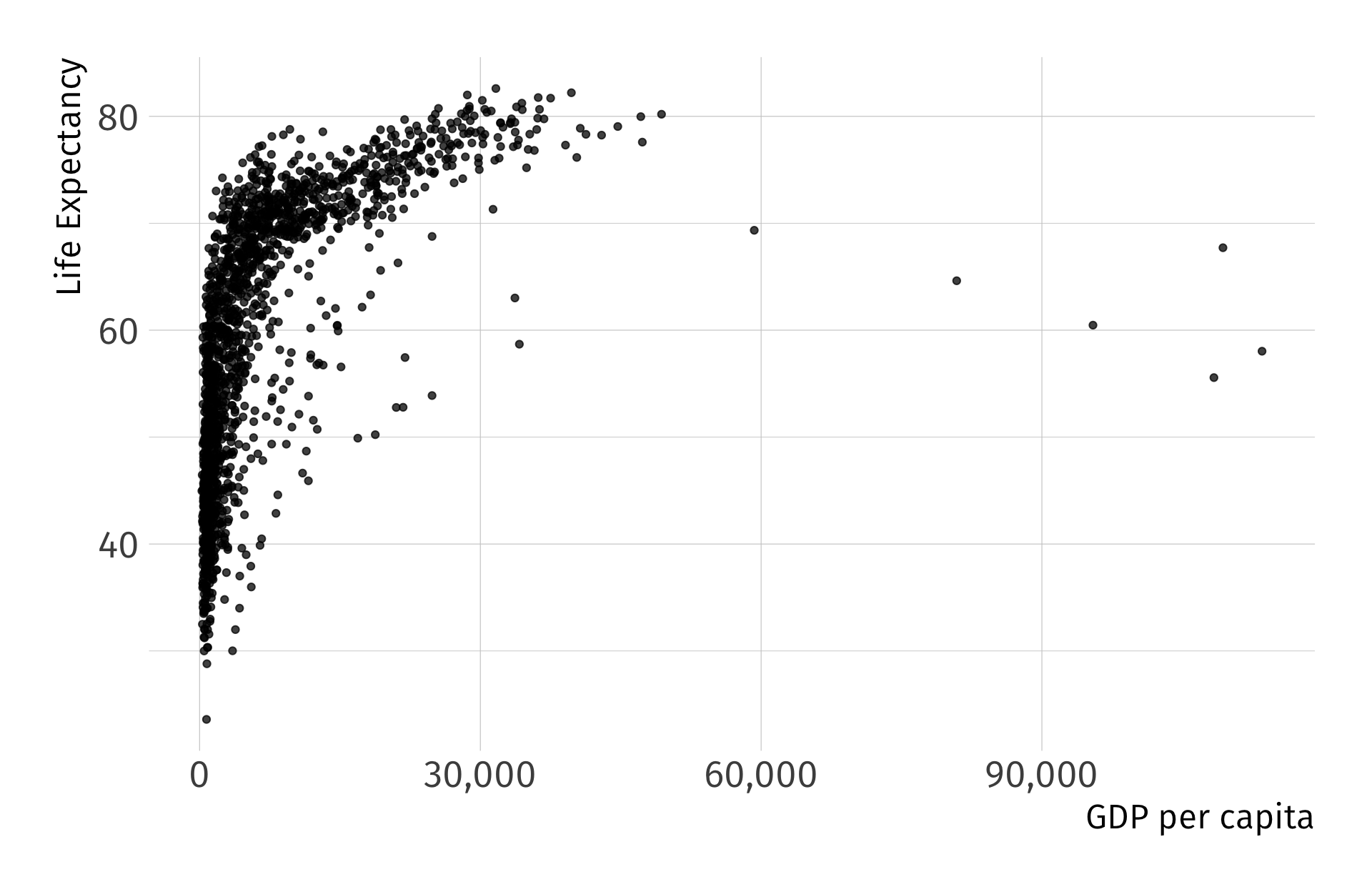
Linear regression

Using the gapminder, we could quickly generate estimates for

\[ \widehat{\text{Life Expectancy}_i} = \hat{\beta_0} + \hat{\beta_1} \cdot \text{GDP}_i \]


library(gapminder)
library(broom)

m1 = lm(lifeExp ~ gdpPercap, data = gapminder) 

tidy(m1)
# A tibble: 2 × 5
  term         estimate std.error statistic   p.value
  <chr>           <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept) 54.0      0.315         171.  0        
2 gdpPercap    0.000765 0.0000258      29.7 3.57e-156

Fitting OLS. But are you satisfied? Can we do better?

Linearity in OLS

Up to this point, we’ve acknowledged OLS as a “linear” estimator.


Many economic relationships are nonlinear.

  • e.g., most production functions, profit, diminishing marginal utility, tax revenue as a function of the tax rate, etc.


The “linear” in simple linear regression refers to the linearity of the parameters or coefficients, not the predictors themselves.

Linearity in OLS

OLS is flexible and can accommodate a subset of nonlinear relationships.

  • Underlying model must be linear-in-parameters.
  • Nonlinear transformations of variables are okay.
  • Modeling some nonlinear relationships requires advanced estimation techniques, such as maximum likelihood1


Put different, independent variables can be a linear combination of the parameters, regardless of any nonlinear transformations

Linearity

Linear-in-parameters: Parameters enter model as a weighted sum, where the weights are functions of the variables.

  • One of the assumptions required for the unbiasedness of OLS.

Linear-in-variables: Variables enter the model as a weighted sum, where the weights are functions of the parameters.

  • Not required for the unbiasedness of OLS.

The standard linear regression model satisfies both properties:

\[Y_i = \beta_0 + \beta_1X_{1i} + \beta_2X_{2i} + \dots + \beta_kX_{ki} + u_i\]

Linearity

Which of the following are an example of linear-in-parameters, linear-in-variables, or neither?


1. \(Y_i = \beta_0 + \beta_1X_{i} + \beta_2X_{i}^2 + \dots + \beta_kX_{i}^k + u_i\)

2. \(Y_i = \beta_0X_i^{\beta_1}v_i\)

3. \(Y_i = \beta_0 + \beta_1\beta_2X_{i} + u_i\)

Linearity

Which of the following are an example of linear-in-parameters, linear-in-variables, or neither?


1. \(\color{#A3BE8C}{Y_i = \beta_0 + \beta_1X_{i} + \beta_2X_{i}^2 + \dots + \beta_kX_{i}^k + u_i}\)

2. \(Y_i = \beta_0X_i^{\beta_1}v_i\)

3. \(Y_i = \beta_0 + \beta_1\beta_2X_{i} + u_i\)


Model 1 is linear-in-parameters, but not linear-in-variables.

Linearity

Which of the following are an example of linear-in-parameters, linear-in-variables, or neither?


1. \(\color{#A3BE8C}{Y_i = \beta_0 + \beta_1X_{i} + \beta_2X_{i}^2 + \dots + \beta_kX_{i}^k + u_i}\)

2. \(\color{#434C5E}{Y_i = \beta_0X_i^{\beta_1}v_i}\)

3. \(Y_i = \beta_0 + \beta_1\beta_2X_{i} + u_i\)


Model 1 is linear-in-parameters, but not linear-in-variables.

Model 2 is neither.

Linearity

Which of the following are an example of linear-in-parameters, linear-in-variables, or neither?


1. \(\color{#A3BE8C}{Y_i = \beta_0 + \beta_1X_{i} + \beta_2X_{i}^2 + \dots + \beta_kX_{i}^k + u_i}\)

2. \(\color{#434C5E}{Y_i = \beta_0X_i^{\beta_1}v_i}\)

3. \(\color{#B48EAD}{Y_i = \beta_0 + \beta_1\beta_2X_{i} + u_i}\)


Model 1 is linear-in-parameters, but not linear-in-variables.

Model 2 is neither.

Model 3 is linear-in-variables, but not linear-in-parameters.

Logarithms

We’re going to take logs

The natural log is the inverse function for the exponential function:

\[ \quad \log(e^x) = x \quad \text{for} \quad x>0 \]

(Natural) Log rules:

1. Product rule: \(\log(AB) = \log(A) + \log(B)\).

2. Quotient rule: \(\log(A/B) = \log(A) - \log(B)\).

3. Power rule: \(\log(A^B) = B \cdot \log(A)\).

4. Derivative: \(f(x) = \log(x)\) => \(f'(x) = \dfrac{1}{x}\).

Note: \(\log(e) = 1\), \(\log(1) = 0\), and \(\log(x)\) is undefined for \(x \leq 0\).

Log-Linear model

Nonlinear Model

\[ Y_i = \alpha e^{\beta_1 X_i}v_i \]

  • \(Y > 0\), \(X\) is continuous, and \(v_i\) is a multiplicative error term.
  • Cannot estimate parameters with OLS directly.

Logarithmic Transformation

\[ \log(Y_i) = \log(\alpha) + \beta_1 X_i + \log(v_i) \]

Redefine \(\log(\alpha) \equiv \beta_0\), \(\log(v_i) \equiv u_i\).

Transformed (Linear) Model

\[ \log(Y_i) = \beta_0 + \beta_1 X_i + u_i \]

Can estimate with OLS, but interpretation changes.

Log-Linear model

Regression Model

\[ \log(Y_i) = \beta_0 + \beta_1 X_i + u_i \]

Interpretation

  • A one-unit increase in the explanatory variable increases the outcome variable by approximately \(\beta_1\times 100\) percent, on average.
Ex.

If \(\log(\hat{\text{Pay}_i}) = 2.9 + 0.03 \cdot \text{School}_i\), then an additional year of schooling increases pay by approximately 3 percent, on average.

Log-Linear model

Derivation Consider the log-linear model

\[ \log(Y) = \beta_0 + \beta_1 \, X + u \]

and differentiate

\[ \dfrac{dY}{Y} = \beta_1 dX \]

Marginal change in \(X\) (\(dX\)) leads to a \(\beta_1 dX\) proportionate change in \(Y\).

  • Multiply by 100 to get the percentage change in \(Y\).

Log-Linear Ex.

\(\log(\hat{Y_i}) = 10.02 + 0.73 \cdot \text{X}_i\)

Log-Linear Ex.

\(\log(\hat{Y_i}) = 10.02 + 0.73 \cdot \text{X}_i\)

Log-Linear model

Note: If you have a log-linear model with a binary indicator variable, the interpretation of the coefficient on that variable changes. Consider

\[ \log(Y_i) = \beta_0 + \beta_1 X_i + u_i \]

for binary variable \(X\).

Interpretation of \(\beta_1\):

  • When \(X\) changes from 0 to 1, \(Y\) will increase by \(100 \times \left( e^{\beta_1} -1 \right)\)%
  • When \(X\) changes from 1 to 0, \(Y\) will decrease by \(100 \times \left( e^{-\beta_1} -1 \right)\)%

Log-Linear Ex.

Binary explanatory variable: trained

  • trained == 1 if employee received training.
  • trained == 0 if employee did not receive training.
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    9.94     0.0446    223.   0       
2 trained        0.557    0.0631      8.83 4.72e-18

Q. How do we interpret the coefficient on trained?

A1: Trained workers 74.52 percent more productive than untrained workers.

A2: Untrained workers 42.7 percent less productive than trained workers.

Log-Log model

Nonlinear Model

\[ Y_i = \alpha X_i^{\beta_1}v_i \]

  • \(Y > 0\), \(X > 0\), and \(v_i\) is a multiplicative error term.
  • Cannot estimate parameters with OLS directly.

Logarithmic Transformation

\[ \begin{align*} \log(Y_i) = \log(\alpha) +& \beta_1 \log(X_i) \\ +& \log(v_i) \end{align*} \]

  • Redefine \(\log(\alpha) \equiv \beta_0\), \(\log(v_i) \equiv u_i\).

Transformed (Linear) Model

\[ \log(Y_i) = \beta_0 + \beta_1 \log(X_i) + u_i \]

Can estimate with OLS, but interpretation changes.

Log-Log regression model

\[ \log(Y_i) = \beta_0 + \beta_1 \log(X_i) + u_i \]

Interpretation

  • A one-percent increase in the explanatory variable leads to a \(\beta_1\)-percent change in the outcome variable, on average.
  • Often interpreted as an elasticity.
Ex.

If \(\log(\widehat{\text{Quantity Demanded}}_i) = 0.45 - 0.31 \cdot \log(\text{Income}_i)\), then each one-percent increase in income decreases quantity demanded by 0.31 percent.

Log-Log derivation

Consider the log-log model

\[ \log(Y_i) = \beta_0 + \beta_1 \log(X_i) + u \]

and differentiate

\[ \dfrac{dY}{Y} = \beta_1 \dfrac{dX}{X} \]

A one-percent increase in \(X\) leads to a \(\beta_1\)-percent increase in \(Y\).

  • Rearrange to show elasticity interpretation:

\[ \dfrac{dY}{dX} \dfrac{X}{Y} = \beta_1 \]

Log-Log Example

\[ \log(\hat{Y_i}) = 0.01 + 2.99 \cdot \log(\text{X}_i) \]

Log-Log Example

\[ \log(\hat{Y_i}) = 0.01 + 2.99 \cdot \log(\text{X}_i) \]

Linear-Log Model

Nonlinear Model

\[ e^{Y_i} = \alpha X_i^{\beta_1}v_i \]

  • \(X > 0\) and \(v_i\) is a multiplicative error term.
  • Cannot estimate parameters with OLS directly.

Logarithmic Transformation

\[ Y_i = \log(\alpha) + \beta_1 \log(X_i) + \log(v_i) \]

Redefine \(\log(\alpha) \equiv \beta_0\), \(\log(v_i) \equiv u_i\).

Transformed (Linear) Model

\[ Y_i = \beta_0 + \beta_1 \log(X_i) + u_i \]

Can estimate with OLS, but interpretation changes.

Linear-Log Model

Regression Model

\[ Y_i = \beta_0 + \beta_1 \log(X_i) + u_i \]

Interpretation

  • A one-percent increase in the explanatory variable increases the outcome variable by approximately \(\beta_1 \div 100\), on average.
Ex.

If \(\hat{(\text{Blood Pressure})_i} = 150 - 9.1 \log(\text{Income}_i)\), then a one-percent increase in income decrease blood pressure by 0.091 points.

Linear-Log derivation

Consider the log-linear model

\[ Y = \beta_0 + \beta_1 \log(X) + u \]

and differentiate

\[ dY = \beta_1 \dfrac{dX}{X} \]

A one-percent increase in \(X\) leads to a \(\beta_1 \div 100\) change in \(Y\).

Linear-Log Example

\[ \hat{Y_i} = 0 + 0.99 \cdot \log(\text{X}_i) \]

Linear-Log Example

\[ \hat{Y_i} = 0 + 0.99 \cdot \log(\text{X}_i) \]

(Approximate) Coefficient Interpretation

Model \(\beta_1\) Interpretation
Level-level
\(Y_i = \beta_0 + \beta_1 X_i + u_i\) 		\(\Delta Y = \beta_1 \cdot \Delta X\)
A one-unit increase in \(X\) leads to a
\(\beta_1\)-unit increase in \(Y\)
Log-level
\(\log(Y_i) = \beta_0 + \beta_1 X_i + u_i\) 		\(\%\Delta Y = 100 \cdot \beta_1 \cdot \Delta X\)
A one-unit increase in \(X\) leads to a
\(\beta_1 \cdot 100\)-percent increase in \(Y\)
Log-log
\(\log(Y_i) = \beta_0 + \beta_1 \log(X_i) + u_i\) 		\(\%\Delta Y = \beta_1 \cdot \%\Delta X\)
A one-percent increase in \(X\) leads to a
\(\beta_1\)-percent increase in \(Y\)
Level-log
\(Y_i = \beta_0 + \beta_1 \log(X_i) + u_i\) 		\(\Delta Y = (\beta_1 \div 100) \cdot \%\Delta X\)
A one-percent increase in \(X\) leads to a
\(\beta_1 \div 100\)-unit increase in \(Y\)

Can We Do Better?

\[ (\widehat{\text{Life Expectancy})_i} = 53.96 + 8\times 10^{-4} \cdot \text{GDP}_i \quad\quad R^2 = 0.34 \]

Can We Do Better?

\[ \log( \widehat{\text{Life Expectancy}_i}) = 3.97 + 1.3\times 10^{-5} \cdot \text{GDP}_i \quad\quad R^2 = 0.3 \]

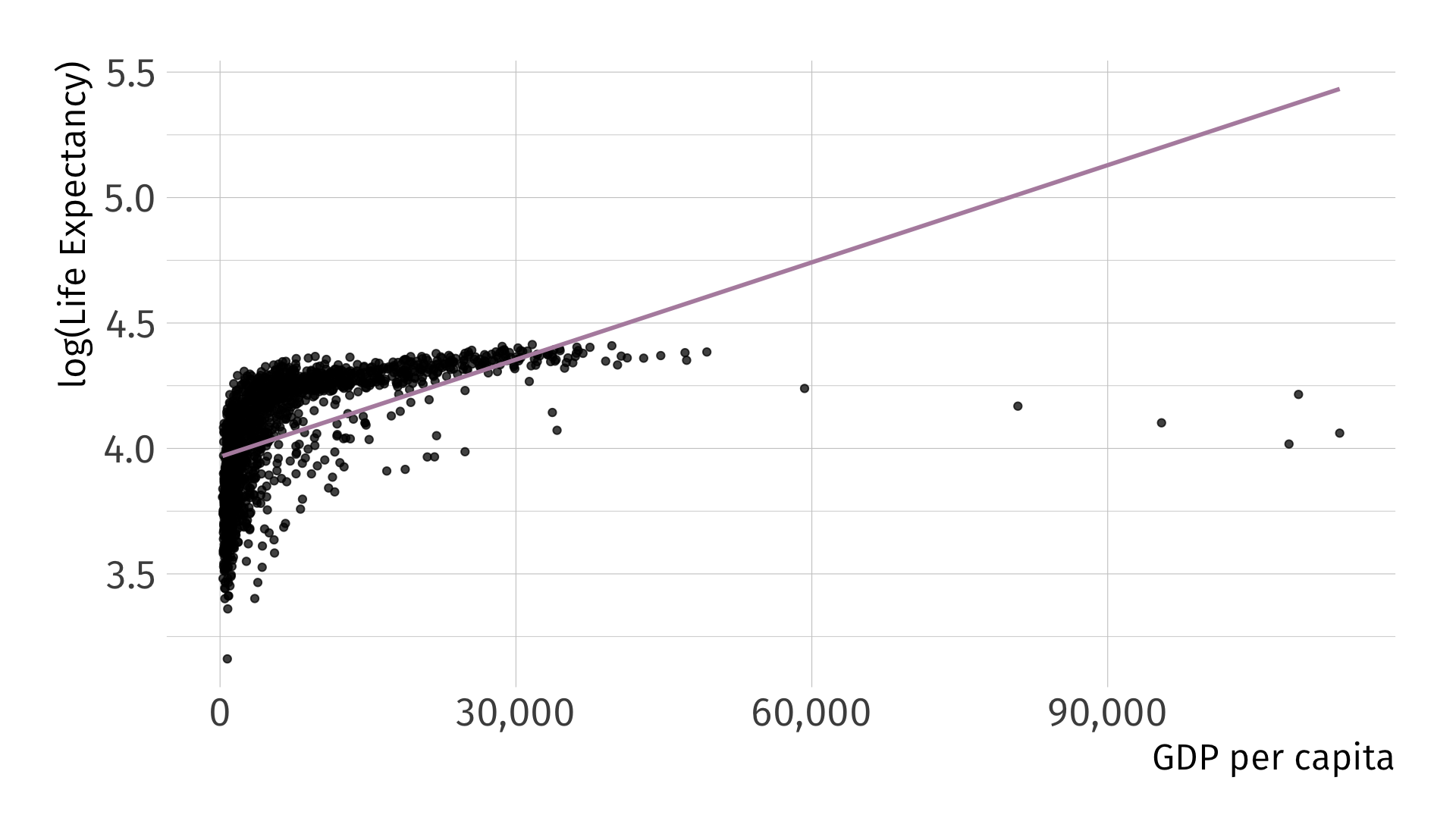
Can We Do Better?

\[ \log ( \widehat{\text{Life Expectancy}_i} ) = 2.86 + 0.15 \cdot \log \left( \text{GDP}_i \right) \quad\quad R^2 = 0.61 \]

Can We Do Better?

\[ ( \widehat{\text{Life Expectancy}})_i = -9.1 + 8.41 \cdot \log \left( \text{GDP}_i \right) \quad\quad R^2 = 0.65 \]

Practical Considerations

Consideration 1 Do your data take negative numbers or zeros as values?

log(0)
[1] -Inf

Consideration 2 What coefficient interpretation do you want? Unit change? Unit-free percent change?

Consideration 3 Are your data skewed?

Quadratic terms

Quadratic variables

Let’s talk about a wage regression again. Suppose we would like to estimate the effect of age on earnings. We estimate the following SLR:

\[ \text{Wage}_i = \beta_0 + \beta_1 \text{Age}_i + u_i \]

However, maybe we believe that \(\text{Wage}_i\) and \(\text{Age}_i\) have some nonlinear relationship—the effect of an additional year of experience, when age is 27 vs age is 67, might be different. So instead, we might estimate:

\[ \text{Wage}_i = \beta_0 + \beta_1 \text{Age}_i + \beta_2 \text{Age}^2_i + u_i \]

Quadratic variables

In this model:

\[ \text{Wage}_i = \beta_0 + \beta_1 \text{Age}_i + \beta_2 \text{Age}^2_i + u_i \]

the effect of \(\text{Age}_i\) on \(\text{Wage}_i\) would be:

\[ \frac{\partial \text{Wage}_i}{\partial \text{Age}_i} = \beta_1 + 2\beta_2 \text{Age}_i \]

Quadratic data

Quadratic regression

Regression Model

\[ Y_i = \beta_0 + \beta_1 X_i + \beta_2 X_i^2 + u_i \]

Interpretation

Sign of \(\beta_2\) indicates whether the relationship is convex (+) or concave (-)

Sign of \(\beta_1\)? 🤷

Partial derivative of \(Y\) wrt. \(X\) is the marginal effect of \(X\) on \(Y\):

\[ \color{#B48EAD}{\dfrac{\partial Y}{\partial X} = \beta_1 + 2 \beta_2 X} \]

  • Effect of \(X\) depends on the level of \(X\)

Quadratic regression

# A tibble: 3 × 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept) 30046.    138.         218.  0        
2 x             159.      5.81        27.3 2.58e-123
3 I(x^2)         -1.50    0.0564     -26.6 6.19e-118

What is the marginal effect of \(\color{#B48EAD}{X}\) on \(\color{#B48EAD}{Y}\)? . . .
\(\widehat{\dfrac{\partial \text{Y}}{\partial \text{X}} } = \hat{\beta}_1 + 2\hat{\beta}_2 X = 158.89 + -3X\)

Quadratic regression

# A tibble: 3 × 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept) 30046.    138.         218.  0        
2 x             159.      5.81        27.3 2.58e-123
3 I(x^2)         -1.50    0.0564     -26.6 6.19e-118

What is the marginal effect of \(\color{#B48EAD}{X}\) on \(\color{#B48EAD}{Y}\) when \(\color{#B48EAD}{X=0}\)?


\(\widehat{\dfrac{\partial \text{Y}}{\partial \text{X}} }\Bigg|_{\small \text{X}=0} = \hat{\beta}_1 = 158.89\)

Quadratic regression

# A tibble: 3 × 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept) 30046.    138.         218.  0        
2 x             159.      5.81        27.3 2.58e-123
3 I(x^2)         -1.50    0.0564     -26.6 6.19e-118

What is the marginal effect of \(\color{#B48EAD}{X}\) on \(\color{#B48EAD}{Y}\) when \(\color{#B48EAD}{X=2}\)?


\(\widehat{\dfrac{\partial \text{Y}}{\partial \text{X}} }\Bigg|_{\small \text{X}=2} = \hat{\beta}_1 + 2\hat{\beta}_2 \cdot (2) = 158.89 -5.99 = 152.9\)

Quadratic regression

# A tibble: 3 × 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept) 30046.    138.         218.  0        
2 x             159.      5.81        27.3 2.58e-123
3 I(x^2)         -1.50    0.0564     -26.6 6.19e-118

What is the marginal effect of \(\color{#B48EAD}{X}\) on \(\color{#B48EAD}{Y}\) when \(\color{#B48EAD}{X=7}\)? . . .
\(\widehat{\dfrac{\partial \text{Y}}{\partial \text{X}} }\Bigg|_{\small \text{X}=7} = \hat{\beta}_1 + 2\hat{\beta}_2 \cdot (7) = 158.89 -20.98 = 137.91\)

Fitted regression line

Marginal effect of \(X\) on \(Y\)

Quadratic regression

Where does the regression \(\hat{Y_i} = \hat{\beta}_0 + \hat{\beta}_1 X_i + \hat{\beta}_2 X_i^2\) turn?

Step 1: Take the derivative and set equal to zero.

\[ \widehat{\dfrac{\partial \text{Y}}{\partial \text{X}} } = \hat{\beta}_1 + 2\hat{\beta}_2 X = 0 \]

Step 1: Solve for \(X\).

\[ X = -\dfrac{\hat{\beta}_1}{2\hat{\beta}_2} \]

Ex. Peak of previous regression occurs at \(X = 53.02\).

Extra: Anscombe’s Quartet

Anscombe’s Quartet

Four “identical” regressions: Intercept = 3, Slope = 0.5, R2 = 0.67

EC320, Set 08 | Nonlinear models